FoxCalculators - Kalkulator Gratis Online!

Dalam matematika, hiperbola jamak atau hiperbola atau hiperbola adalah jenis kurva halus, ia memiliki dua bagian, dinamai sebagai komponen atau cabang, mereka menyerupai dua busur tak terbatas satu sama lain. hiperbola berbaring di pesawat.

Formula Hyperbola:

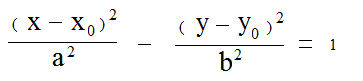
Grafik Hyperbola:

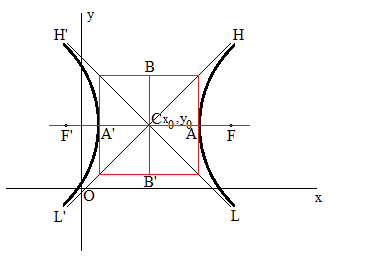
Persamaan dan grafik hyperbola dengan pusat C (x _{0 , y 0 ) dan poros utama paralel dengan sumbu x. Jika sumbu utama sejajar dengan sumbu Y, pertukaran X dan Y selama perhitungan.}

Persamaan Kalkulator Hyperbola:

Hyperbola Fokus F x Coordinate = x _{0 + √ (A ^{2 + B 2 )}}

Hyperbola Focus F Y Koordinat = Y ₀

Hiperbola fokus f 'x koordinat = x _{0 - √ (A ^{2 + B 2 )}}

Hyperbola Focus F 'Y Koordinat = Y ₀

Asimptot h'l: y = (b / a) x + y _{0 - (b / a) x 0}

Asimptotes lh ': y = (- b / a) x + y _{0 + (b / a) x 0}

Hiperbola eksentrisitas = √ ( ^{2 + B 2 ) / a}